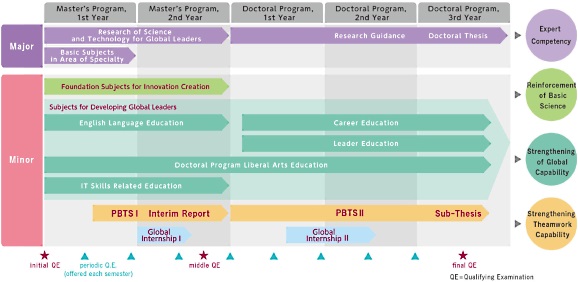
Class List of Fall Semester 2017
“Essential Mathematics for Global LeadersⅡ” is offered as Intensive Course. This is a class for students in “Minor Course of Science and Technology for Global Leaders”. But all master’s & doctoral students can take it if you have interest. The class will be conducted in English.
Theme & Objective
Theme: Differential Equations (in the broader sense of dynamical systems) are the core topics in mathematical modeling.
Objective: Through examples in Mathematica to understand
-
what are Ordinary, Partial Differential Equations (ODE, PDE)
-
some methods of resolution: closed forms, Series Solutions, Fourier & Laplace Transforms…
-
how to use Mathematica to solve and visualize solutions.
Message to Students
As part of the Essential course series, Essential Maths I (Statistics) and II (modeling ODE and PDE) are supposed to endow/increase capability to model concrete problems with mathematical equations. Essential Math II focuses on the use of a math software, and through its visualization functionality to learn/put into practice basic methods of resolution. Mathematical notions will be introduced formally, but main theorems will be stated in a concrete way. Most proofs will be omitted, in particular only basic notions of Calculus and of Linear Algebra are expected for this course.
Lecture Outline
| Subject |
|---|
| Essential Mathematics for Global LeadersⅡ [17S1007] |
| Number of Credits |
| 2.0 |
| Instructor |
| Dahan, Xavier (Project Associate Professor of Ochanomizu University) |
| Target Audience |
| Graduate Students |
| Location |
| Graduate School of Humanities & Sciences Building R408 |
| Date & Time |
|
This class is held as Intensive Course. Year 2018 February 14, Wednesday Period 5-8 (13:20-16:30) February 16, Friday Period 3-4 (10:40-12:10) February 19, Monday Period 5-8 (13:20-16:30) February 21, Wednesday Period 5-8 (13:20-16:30) February 22, Thursday Period 5-8 (13:20-16:30) February 23, Friday Period 3-4 (10:40-12:10) February 27, Tuesday Period 5-8 (13:20-16:30) March 1, Thursday Period 5-8 (13:20-16:30) |
| Lecture Types |
| Lecture, computer practice. |
| Lecture Plan |
|
Content: Introduction to mathematical modeling with Mathematica The following topics will be introduced, (maybe not exactly in this order !). All topics are illustrated with Examples and some small projects in Mathematica. 0. Introduction to Mathematica. Mathematica
1. Continuous differential systems.
2. Discrete differential systems (finite-difference systems).
3. Partial Differential Equations. |
| Textbook/Reference |
|
a) Dynamical Systems with applications using Mathematica (S. Lynch, Birkhauser 2007) b) Introduction to Partial Differential Equations for Scientists and Engineers Using Mathematica (Kuzman Adzievski, Abul Hasan Siddiqi. Taylor & Francis, 2013) |
Registration
Registration Period: Mon., October 2 through Sat., October 14
If you cannot register during above period, please contact Academic Affairs Office in Student Affairs Building.
Contact
Ochanomizu University Leading Graduate School Promotion Center
Tel: 03-5978-5775
E-mail:
